Week 1 Notes
STAT 251 Section 03
Lecture 1: Wednesday Jan. 10th 2024
Introduction to statistical methods
Data, observations, variables
Statistics is a scientific field that deals with the collection, description, analysis, interpretation, and presentation of data. We see and use data in nearly all aspects of our everyday lives: politics, medicine, forecasting, finance, marketing, etc. In short, we use statistics to ask and answer scientific questions and make predictions. To put it another way, statistics is the science of data
data are pieces of factual information, such as measurements which are recorded and used for the purpose of analysis. In summary, data is the raw information from which statistics are created. Statistics are the results of data analysis - its interpretation and presentation.
Typically data are represented in a square table called a data table. The fundamental unit of data is an observation - a single row of a data table representing a set of measurements on one or more variables.
A variable is a characteristic of an observation. In a typical data table, the variables are represented by the columns of the data table.
The following example are fictional data consisting of 20 observations of the height, age, and blaster accuracy of stormtroopers graduating from the imperial stormtrooper academy.
| Identification Number | Duty Posting | Height (cm) | Age | Blaster Accuracy | Rank |
|---|---|---|---|---|---|
| FN-2414 | Berchest Station | 184.9 | 19 | 0.62 | PV1 |
| FN-2462 | Death Star | 193.3 | 20 | 0.66 | PV2 |
| FN-2178 | Death Star | 191.0 | 20 | 0.77 | CPL |
| FN-2525 | Lothal | 186.7 | 23 | 0.61 | PFC |
| FN-2194 | Corellia | 194.6 | 21 | 0.66 | PV1 |
| FN-2937 | Fondor Ship Yard | 191.9 | 22 | 0.75 | PV2 |
| FN-2817 | Fondor Ship Yard | 189.5 | 21 | 0.59 | CPL |
| FN-2117 | Death Star | 193.5 | 21 | 0.66 | PFC |
| FN-2298 | Corellia | 193.4 | 24 | 0.66 | PV1 |
| FN-2228 | Berchest Station | 193.2 | 21 | 0.71 | PV2 |
| FN-2243 | Death Star | 192.8 | 24 | 0.69 | CPL |
| FN-2013 | Corellia | 192.3 | 18 | 0.62 | PFC |
| FN-2373 | Lothal | 190.3 | 22 | 0.60 | PV1 |
| FN-2664 | Berchest Station | 189.5 | 21 | 0.72 | PV2 |
| FN-2601 | Fondor Ship Yard | 189.2 | 21 | 0.73 | CPL |
| FN-2602 | Lothal | 188.2 | 22 | 0.62 | PFC |
| FN-2767 | Death Star | 189.8 | 20 | 0.76 | PV1 |
| FN-2708 | Death Star | 186.3 | 20 | 0.61 | PV2 |
| FN-2090 | Fondor Ship Yard | 197.7 | 19 | 0.64 | CPL |
| FN-2952 | Corellia | 194.5 | 19 | 0.57 | PFC |
The following are 15 observations of study done on the morphology of Egyptian skulls from 5 epochs of Egyptian history. For each skull, the epoch, and several measurements characterizing the shape of the skull are recorded.
| Epoch | maximal breadth | basiregmatic height | basilveolar length | nasal height |
|---|---|---|---|---|
| c200BC | 139 | 130 | 94 | 53 |
| c3300BC | 131 | 134 | 96 | 50 |
| c4000BC | 131 | 138 | 89 | 49 |
| c4000BC | 124 | 138 | 101 | 46 |
| c200BC | 135 | 131 | 99 | 51 |
| c4000BC | 131 | 134 | 97 | 54 |
| c1850BC | 133 | 131 | 96 | 49 |
| c3300BC | 129 | 126 | 91 | 50 |
| c4000BC | 132 | 131 | 101 | 49 |
| c200BC | 133 | 136 | 95 | 52 |
| c200BC | 141 | 130 | 87 | 49 |
| c3300BC | 126 | 131 | 100 | 48 |
| c200BC | 129 | 135 | 95 | 47 |
| c4000BC | 135 | 135 | 103 | 47 |
| c3300BC | 131 | 139 | 98 | 51 |
Types of variables
Variables are distinguished by the type of information they represent. One basic distinction is between qualitative variables and quantitative variables.
qualitative variables - also called categorical variables, represent non numeric qualities or characteristics that can be placed in distinct categories. What are the qualitative variables in the stormtrooper data above?
quantitative variables - Sometimes referred to as numeric variables, are numerical characteristics which have an inherent order or ranking. In the Egyptian skull data which variables are quantitative variables?
Qualitative variables can be further divided between nominal and ordinal variables.
nominal variables - non numeric qualities or characteristics that can be placed in distinct categories that do not have a natural ordering. Examples of variables that cannot be ordered are gender, race, eye color, or political party. In the stormtrooper data, which variables would be considered nominal variables?
ordinal variables - non numeric qualities or characteristics that can be placed in distinct categories with an inherent ordering. Examples include education level (i.e bachelors, masters, PhD) or temperatures (i.e cool, warm, hot).
- Likert scale responses are a common example of ordinal variables that are typically found in surveys. A Likert scale is a rating scale used to measure opinions, attitudes, or behaviors. It consists of a statement or a question, followed by a series of five or seven answer statements. Respondents choose the option that best corresponds with how they feel about the statement or question.
Quantitative variables can also be further divided between two sub-categories: discrete and continuous variables.
discrete variables - are quantitative variables that take on distinct, countable values (i.e whole numbers or integers) such \(0,1,2,3 ...\). Any quantitative variable that represents counts of objects/items are quantitative discrete. For example, age is a count of the number of year someone/something has been alive.
continuous variables - are variables that can take on infinite number of values within an interval of any two specific values (e.g temperature \(^{\circ} C / ^{\circ} F\), height in inches, speed in miles per hour).
Populations and samples
Statistics is generally concerned with studying properties of a population. You can think of a population as a collection of all possible persons, things, or objects that you are studying. Another way to think of a population is as a collection of all possible observations of a variable - both observed and unobserved.
- A population can be finite (countable) or infinite (uncountable). Many populations are so large that we treat them as if they are infinite. For example, the population of students taking STAT 251 section 03 is a finite set of 60 individuals. Alternatively, the number of germs living in a patients body is effectively infinite.
For many populations, it is very difficult or even impossible to observe all members of the population. To tackle this challenge statistics uses samples to learn about the properties of a population. A sample is a subset of the population that is actually observed. You can think of a sample as a set of the observed observations.
The idea of sampling is to select a portion of individuals or objects that are representative of the population
To illustrate the distinction between a sample and a population, let’s take the example of a wildlife biologist researching the paw size of mountain lions in the state of Idaho. In this scenario, the population being examined encompasses all the mountain lions residing in the state, totaling approximately 2,000 individuals. However, due to the considerable challenges and expenses associated with tracking and observing every existing member, the biologist opts to document the paw size of a more manageable subset of 20 mountain lions. The 20 mountain lions for which the biologist records paw sizes constitute a sample from the larger population of mountain lions.
In statistics we typically represent the size (i.e number of observations) of a population with the letter \(N\) and the size of a sample with the letter \(n\). In the above example of the wildlife biologist studying mountain lion paw size, the population has size \(N = 2,000\) and the sample the biologist took was of size \(n = 20\).
Statistics vs. Parameters
Statistics primarily deals with estimation – the process of inferring an unknown quantity about a population using set of sample data. An estimator is a mathematical function that estimates a given statistic based on observed data.
- Therefore, a statistic is a numerical characteristic of a sample that represents a property of the population called a parameter. Parameters are numerical characteristics of a population that can be estimated via a statistic.
We will use Greek letters such as \(\theta, \sigma, \mu\) to represent parameters. These symbols with “hats” like \(\hat{\theta}, \hat{\sigma}, \hat{\mu}\) are used to represent estimators/statistics.
Two statistics that we will deal with in this course are the sample mean and sample proportion.
A proportion describes the fraction of a whole that represent some property or category. It can be expressed as a value between \(0\) and \(1\) or as a percentage. The sample proportion \(\hat{p}\) is the fraction of observations in the sample that represent a particular category. The population proportion is the fraction of observations in the population that represent a particular category. The sample proportion is defined mathematically as \[ \hat{p} = \frac{\text{Number of observed observations in category}}{n}\] The population proportion is defined mathematically as \[ \hat{p} = \frac{\text{All observations in category}}{N}\] The sample proportion \(\hat{p}\) is used to estimate the population proportion \(p\)
The arithmetic mean (sometimes called average) describes the center of a population or set of data. The sample mean \(\bar{x}\) describes the central tendency of the observation in the sample. The population mean describes the central tendency of the entire population. The sample mean is defined mathematically as \[\bar{x} = \sum_{i = 1}^{n} \frac{x_i}{n}\] The population mean is defined mathematically as \[ \mu = \sum_{i = 1}^{N} \frac{x_i}{N}\] The sample mean \(\bar{x}\) is used to estimate the population mean \(\mu\)
The tools for estimation allow us to approximate almost everything about populations using only samples. With estimates we can:
- Assess differences among groups and relationships between variables.
- Describe populations. Examples of estimates include averages, proportions, measures of variation, and measures of relationship.
- Then we can ask and answer questions or formally, test and evaluate hypotheses.
Descriptive vs Inferential Statistics
Recall that statistics is a science that deals with the collection, description, analysis, interpretation, and presentation of data. The collection of data is referred to as the design. In statistics, design concerns the formulation of statistical questions and the process/method in which we plan to collect data to answer our statistical question.
Descriptive statistics - refers to a organizational step that occurs before we do any analysis or make any decisions/predictions. It includes describing the observations in a sample using statistics or describing a population using parameters. It can also include graphical summaries of a sample or population.
Inferential statistics - refers to using a sample (usually a statistic) to answer a question about a population such as estimating the value of a parameter. It includes estimating parameters, making decisions, and prediction.
Key Point: Descriptive statistics can be applied to samples or populations. Inferential statistics are only applied to samples in order to make inferences about a population.
Lecture 2: Friday, Jan. 12th 2024
Describing and Visualizing Distributions
As we learned in the previous lecture, descriptive statistics is the first step to statistical analysis and involves the summary and organization of data. One of the main ways we can summarize data is describe the characteristics of the distribution of the variable(s) in the data. A distribution tells us something about what kinds of values a variable can have and how often they occur.
- Consider the following example: Are teens distracted by their cell phones? A study conducted by the Pew Research center surveyed 743 U.S teenagers ages 13-17 to understand how cell phones in class impacted their ability to concentrate. Each student was asked to rate the impact of cell phone use on their concentration based on a Likert scale. The data and a plot of the distribution of survey responses are given below
| Student | Age | Response |
|---|---|---|
| 1 | 13 | Never |
| 2 | 13 | Sometimes |
| 3 | 15 | Never |
| 4 | 17 | Often |
| \(\vdots\) | \(\vdots\) | \(\vdots\) |
| 743 | 16 | Rarely |
- What type of variable is Age?
- What type of variable is Response?
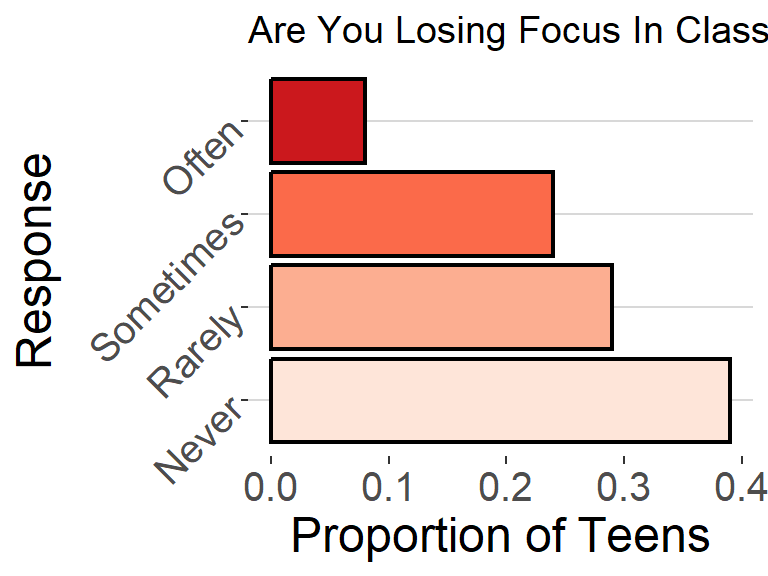
Figure 1. Distribution of student responses to survey question ” Are You Losing Focus In Class By Checking Your Cell Phone? ”
- Looking at the distribution of survey responses above, would you say that most teens feel they are distracted by their cell phones?
Distributions
Formally, a distribution is a function that gives (a) the possible values of a variable and (b) how often each value occurs. The how often is usually described using frequency or relative frequency .
The frequency of a given value is simply a count of the number of times that the given values occurs
The relative frequency of a given value is the proportion of times that the given value occurs
We can also use the cumulative relative frequency to describe how often a variable occurs. The cumulative relative frequency is the proportion of values that are less than or equal to a given value in a distribution.
- Note: As we said with the example about distracted teens, we can talk about the distribution of a categorical variable as well, however we may not use the cumulative relative frequency if there is no natural order to the values (i.e qualitative - nominal).
Consider the following hypothetical set of \(10\) exam scores (out of 10 points) for students in a statistics course \[\{5, 6, 6, 7, 7, 7, 8, 9, 9, 10\}\]
- the possible test scores are \(5, 6, 7, 8,
9,\) and \(10\). Lets try
computing the frequency, relative frequency, and cumulative relative
frequency for students who score a 6 on the exam.
The frequency for an exam score of \(6\) is \(freq(6) = 2\) because \(2\) of the \(10\) students had an exam score of \(6\).
Similarly, the relative frequency for an exam score of \(6\) is \(2/10 = 0.2\).
The cumulative relative frequency for an exam score of \(6\) will be the total number of values in the data that are less than or equal to the value \(6\). This will be the frequency of \(5\)’s plus the frequency of \(6\)’s which will be \((1 + 2)/10 = 3/10\) or \(0.3\). Alternatively we could simply add the relative frequency for an exam score of \(5\) to the relative frequency for an exam score of \(6\): \(0.1 + 0.2 = 0.3\)
| Score | Frequency | Relative Frequency | Cumulative Relative Frequency |
|---|---|---|---|
| 5 | 1 | 0.1 | 0.1 |
| 6 | 2 | 0.2 | 0.3 |
| 7 | 3 | 0.3 | 0.6 |
| 8 | 1 | 0.1 | 0.7 |
| 9 | 2 | 0.2 | 0.9 |
| 10 | 1 | 0.1 | 1.0 |
- The table above is called a frequency table it is a tabular display of the distribution of a variable.