Week 14 Notes
STAT 251 Section 03
Lecture 26 Monday, April 8th 2024
Comparing two means
Last week we learned how to compare two populations across a qualitative response variable by comparing their relative proportions. Now we will learn how we can compare two groups on a quantitative response variable by comparing their means. There are many cases where researchers might be interesting comparing groups across a quantitative variable. For example, a teacher may be interested in comparing the average test scores of students in two different classes (Class A and Class B). A social scientist may be interest in whether there is a difference in salaries between men and women within a company. In any case, we are again dealing with two samples of sizes \(n_1\) and \(n_2\) which come from populations population 1 and population 2 and with means as \(\mu_1\) and \(\mu_2\).
| Population | Population Mean | Population Stdev | Sample Size | Sample Mean | Sample Stdev |
|---|---|---|---|---|---|
| 1 | \(\mu_1\) | \(\sigma_1\) | \(n_1\) | \(\bar{x}_1\) | \(s_1\) |
| 2 | \(\mu_2\) | \(\sigma_2\) | \(n_2\) | \(\bar{x}_2\) | \(s_2\) |
Let \(\mu_d = \mu_1 - \mu_2\) be the mean difference between the two populations. We can construct confidence intervals to estimate the average difference as well as conduct hypothesis tests to determine if two populations are significantly different.
A confidence interval for the mean difference \(\mu_d\)
We will begin by assuming that we are dealing with two independent samples from two distinct populations. The natural estimator of \(\mu_d\) is the difference between the sample means
\[\hat{\mu}_d = \bar{x}_1 - \bar{x}_2\]
To base our inference on the above estimator, we must know its sampling distribution. If we assume that both samples come from populations that are normally distributed, then the distribution of the difference will also be normally distributed and the variances will add:
\[Var[\mu_1 - \mu_2] = \frac{\sigma_1^2}{n_1}+\frac{\sigma_2^2}{n_2}\]
In practice, \(\sigma_1^2\) and \(\sigma_2^2\) are unknown population parameters but can be estimated by substituting in the sample variances \(s_1^2\) and \(s_2^2\). This gives the following standard deviation for the estimator \(\hat{\mu}_d\)
\[SE(\hat{\mu}_d) = \sqrt{\frac{s_1^2}{n_1}+\frac{s_2^2}{n_2}} \]
Just as it was for a single mean, estimating the population variances with the sample variances adds additional uncertainty. Thus, the the sampling distribution for the difference in two means is \(t\)-distributed, although the degrees of freedom are calculated differently. The actual formula for the degrees of freedom is quite messy and difficult to compute:
\[df = \frac{\left(\frac{s_1^2}{n_1}+\frac{s_2^2}{n_2}\right)^2}{ \frac{1}{n_1 - 1}\left(\frac{s_1^2}{n_1}\right)^2 + \frac{1}{n_2-1}\left(\frac{s_2^2}{n_2}\right)^2} \]
We will instead compute the degrees of freedom by taking the smaller of \(n_1-1\) and \(n_2 - 1\) which is a lower bound on the formula above
\[\hat{\mu}_d \sim t(\min(n_1 - 1, n_2 - 1)) \]
The margin of error for estimating the mean difference at the \((1-\alpha)\%\) level is given by
\[m = t_{1-\alpha/2} \times SE(\hat{\mu}_d) \]
which gives the following confidence interval for the mean difference
\[(\bar{x}_1 - \bar{x}_2) \pm t_{1-\alpha/2} \times SE(\hat{\mu}_d)\]
Example: Comparing Customer Satisfaction Levels - Suppose we want to compare the customer satisfaction levels of two competing cable television companies, Company 1 and Company 2. We randomly select customers from each company and ask them to rate their cable companies on a five-point scale (with 1 being least satisfied and 5 most satisfied). The data are summarized in the table below:
| Group | Number of customers | Sample Mean Rating | Sample Stdev |
|---|---|---|---|
| Company 1 | 174 | 4.2 | 0.8 |
| Company 2 | 355 | 3.8 | 1.1 |
Estimate the difference in mean satisfaction levels between the two companies at the \(95\%\) confidence level.
Let \(\mu_1\) represent the mean satisfaction score for company 1 and \(\mu_2\) represent the mean satisfaction score for company 2. The estimated mean difference in customer satisfaction is \[\hat{\mu_d} = 4.2 - 3.8 = 0.4 \]
Since the confidence level is \(95\%\) the standard score will be approximately the \(t_{1-0.05/2} = t_{0.975}\) or the \(97.5th\) percentile of a \(t\)-distribution with \(173\) degrees of freedom. Since the \(t\) and \(z\) distributions are approximately for sample sizes \(\geq 30\) we will use the standard score \(1.96\). The standard error of the difference is given by
\[SE(\hat{\mu}_d) = \sqrt{\frac{0.8^2}{174}+\frac{1.1^2}{355}} =0.0842 \]
Which yields the follow margin of error
\[ m = 1.96 (0.0842) = 0.165\]
The \(95\%\) confidence interval is \([0.24, 0.56]\). Thus, at the \(95\%\) confidence level we estimate the mean difference in customer satisfaction score to be no less than \(0.24\) and no more than \(0.56\). Notice that the above confidence interval does not span zero and thus likely constitutes a real, but small, difference between the companies
A significance test for comparing two means: independent samples
We can also test for a difference between two groups on a quantitative response. variable by comparing their means. The set up for a significance test for a difference in two means is more or less the same as we saw previously for two proportions, however, the calculations now involve \(\bar{x}_1\), \(\bar{x}_2\), \(s_1\) and \(s_2\). Recall that, under the assumption of normality for both populations and when using the sample standard deviations to estimate \(\sigma_1\) and \(\sigma_2\) the difference in means is \(t\)-distributed. We will see that test statistic \(t_{obs}\) is the standardized difference and has approximately the same distribution. Here’s how we set up a two-sample hypothesis test for means:
1. Assumptions
Data constitute a simple random sample
The two groups are independent
Both populations are normally distributed
2. Null and Alternative Hypotheses
- The null hypothesis is generally that the two population means are equal (i.e no difference)
\[H_0: \mu_1 = \mu_2 \ \ \ \text{which is the same as} \ \ \ H_0: \mu_1 - \mu_2 = 0\]
- The alternative hypothesis can be either lower, upper, or two tailed just as it was with our univariate tests. The table below gives the possible alternative hypotheses and their critical values:
| Alternative Hypothesis | Critical Value | Rejection Region |
|---|---|---|
| \(H_A: \mu_1 - \mu_2 \neq 0\) | \(t_{1-\alpha/2}\) | \(|t| \geq t_{1-\alpha/2}\) |
| \(H_A: \mu_1 - \mu_2 < 0\) | \(t_\alpha\) | \(t\leq t_{\alpha}\) |
| \(H_A: \mu_1 - \mu_2 > 0\) | \(t_{1-\alpha}\) | \(t\geq t_{1-\alpha}\) |
3. Test statistic
- Under the null hypotheses the test statistic is the standardized difference
\[t_{obs} = \frac{(\bar{x}_1 - \bar{x}_2) - (\mu_1 - \mu_2)}{\sqrt{\frac{s_1^2}{n_1}+\frac{s_2^2}{n_2}}} \]
The above test statistic is only approximately \(t\)-distributed. However, the lower bound for the degrees of freedom given by \(\min(n_1 - 1, n_2 - 1)\) generally leads to conservative estimates and tests and is thus favorable.
4. \(p\)-value
- The \(p\)-values corresponding to each alternative hypothesis are listed in the table below
| Alternative Hypothesis | \(p\)-value |
|---|---|
| \(H_A: \mu_1 - \mu_2 \neq 0\) | \(P(|t| \geq |t_{obs}||H_0)\) |
| \(H_A: \mu_1 - \mu_2 < 0\) | \(P(t \leq t_{obs}|H_0)\) |
| \(H_A: \mu_1 - \mu_2 > 0\) | \(P(t\geq t_{obs}|H_0)\) |
5. Decision rule
\[\text{Reject} \ \ H_0 \ \ \text{if} \ \ \text{$p$-value} < \alpha \]
The pooled \(t\) test
There is one situation where the above test statistic has exactly a \(t\)-distribution and that occurs when we can assume that both populations have the same standard deviation. In this case, we need only substitute a single sample standard deviation for \(\sigma_1\) and \(\sigma_2\). We call this the pooled estimate of the standard deviation:
\[ s_{pooled} = \sqrt{ \frac{(n_1 - 1)s_1^2 + (n_2 -1)s_2^2}{n_1+n_2 - 2}}\]
\(s_{pooled}\) is called the pooled estimator of \(\sigma_d\) because it combines the information from both samples.
The test statistic under the assumption of equal variances becomes
\[t_{obs} = \frac{(\bar{x}_1 - \bar{x}_2) - (\mu_1 - \mu_2)}{s_{pooled}\sqrt{\frac{1}{n_1}+\frac{1}{n_2}}} \]
which is exactly distributed as a \(t\) distribution with \(n_1+n_2 - 2\) degrees of freedom. The test based on the pooled estimate of the standard deviation is more powerful because the sampling distribution is exact and not an approximation as it is in the unpooled case.
Which test should you use?
- In practice, a significance test for determining equality of variances can be run prior to the \(t\)-test to determine if the pooled or unpooled test statistic should be used. More information about this test can be found here
Example: NCAA Womens Basketball - Sunday April 7th South Carolina and Iowa contended for the NCAA womens basketball championship. Consider the following table which gives the opponent and number of points scored for both teams in their last \(15\) games leading up to the championship.
| South Carolina | Matchup |
|
Iowa | Matchup |
|---|---|---|---|---|
| 78 | NC State | 71 | UConn | |
| 70 | Oregon State | 94 | LSU | |
| 79 | Indiana | 89 | Colorado | |
| 88 | UNC | 64 | West Virginia | |
| 91 | Presbyterian | 91 | Holy Cross | |
| 79 | LSU | 94 | Nebraska | |
| 74 | Tenessee | 95 | Michigan | |
| 79 | Texas A&M | 95 | Penn State | |
| 76 | Tenessee | 93 | Ohio State | |
| 98 | Arkansas | 108 | Minnesota | |
| 103 | Kentucky | 101 | Illinois | |
| 72 | Alabama | 69 | Indiana | |
| 70 | Georgia | 106 | Michigan | |
| 66 | Tenessee | 79 | Nebraska | |
| 83 | UConn | 111 | Penn State |
The summary of the last \(15\) games is given below:
| Population | Population Mean | Sample Size | Sample Mean | Sample Stdev |
|---|---|---|---|---|
| Iowa | \(\mu_1\) | \(n_1 = 15\) | 90.67 | 14.21 |
| South Carolina | \(\mu_2\) | \(n_2 = 15\) | 80.40 | 10.57 |
Conduct a unpooled two sample \(t\)-test at the \(\alpha = 0.05\) significance level to determine if there is a significant difference between the championship teams in the mean number of points scored per game.
- Let \(\mu_1\) be the mean number of points scored per game for Iowa and \(\mu_2\) be the mean number of points score per game for South Carolina. The null hypothesis is that there is no difference in the mean number of points between the two teams
\[H_0: \mu_1 = \mu_2 \]
The alternative hypothesis is that the two teams are different
\[H_A: \mu_1 \neq \mu_2\]
- The estimated difference is given by \(\hat{\mu}_d = \bar{x}_1 - \bar{x}_2 = 10.27\). The test statistic for the unpooled test is
\[ t_{obs} = \frac{90.67 - 80.40}{\sqrt{\frac{14.21^2}{15}+\frac{10.57^2}{15}}} \approx 2.246\]
which is approximately distributed as
\[ t_{obs}\sim t(df = 14) \]
- The pvalue is
\[\text{$p$-value} = 2\left[P(|t| \geq |t_{obs}||H_0)\right] = 2(0.0207) = 0.0414 \]
- Based ont the \(p\)-value above we would narrowly reject the null hypothesis and conclude that Iowa scores significantly more points per game than South Carolina on average. The outcome of the championship was a 75 - 87 victory for South Carolina. Given the conclusion of our test, this is a testament to South Carolina’s defensive prowess in being able to shut down a high scoring team like Iowa.
Lecture 27 Wednesday, April 10th 2024
Paired \(t\) test
Comparative methods (i.e methods that compare two groups/samples across a quantitative variable) are more common and often preferred over one sample procedures. One common comparative design that makes use of single-sample procedures for a population mean is called the paired \(t\)-test. This test is used to draw inferences about a population mean in matched-pairs designs and can be thought of as the parametric analogue of the sign test we learned previously. Recall that in matched-pairs studies subjects are matched based on common characteristics and the quantitative outcome is compared within each pair.
matched-pairs designs are most common when randomization is not possible
often used when observations are taken on the same subject (before and after treatment)
In a paired \(t\)-test we convert a comparative study into a one-sample procedure by making the response variable the difference between the two observations in each pair \(d_i = x_i - y_i\). The parameter under study is the population mean difference \(\mu_d\) which can be estimated by the sample mean difference \(\bar{x}_d = \bar{x} - \bar{y}\) computed over all pairwise differences. The standard deviation of the difference \(\sigma_d\) is then estimated with the sample standard deviation of the difference. Inference is then treated in the same way as one-sample procedures for a population mean
- the \((1 - \alpha)\%\) confidence interval for the mean pairwise difference is
\[ \bar{x}_d \pm t_{1-\alpha/2} \frac{s_d}{\sqrt{n}}\]
- the test statistic for a signifcance test regargin the pairwise difference is given by
\[t_{obs} = \frac{\bar{x}_d - \mu_d}{s_d/\sqrt{n}} \sim t(n - 1) \]
- by treating the above procedure as a one-sample \(t\) test we make the assumption that the population distribution of differences is approximately normal.
Example: Revisting the Spousal Dominance Problem - Recall the study comparing the ratings of husbands and wives on the perceived relative influence of each member of the couple on a major financial decision.
| Couple | Husband | Wife | Difference |
|---|---|---|---|
| 1 | 5 | 3 | 2 |
| 2 | 4 | 3 | 1 |
| 3 | 6 | 4 | 2 |
| 4 | 6 | 5 | 1 |
| 5 | 3 | 3 | 0 |
| 6 | 2 | 3 | -1 |
| 7 | 5 | 2 | 3 |
| 8 | 3 | 3 | 0 |
| 9 | 1 | 2 | -1 |
| 10 | 4 | 3 | 1 |
| 11 | 5 | 2 | 3 |
| 12 | 4 | 2 | 2 |
| 13 | 4 | 5 | -1 |
| 14 | 7 | 2 | 5 |
| 15 | 5 | 5 | 0 |
| 16 | 5 | 3 | 2 |
| 17 | 5 | 1 | 4 |
A summary of the difference in rating between husbands and wives is given below:
| Parameter | Estimate | Stdev |
|---|---|---|
| \(\mu_d\) | 1.35 | 1.77 |
Conduct a paired \(t\)-test at the \(\alpha = 0.05\) significance level to determine if husbands and wives differ in their perceived influence on financial decision making
Statistical Inference for qualitative data
The table below summarizes the procedures we have learned so far in the course
| Parameter | Type | Response Variable | \((1 - \alpha)\%\) CI | Test statistic | Distribution |
|---|---|---|---|---|---|
| \(p\) | one-sample | Categorical | \(\hat{p}\pm Z_{1-\alpha/2}\sqrt{\frac{\hat{p}(1-\hat{p})}{n}}\) | \(\frac{\hat{p} - p_0}{\sqrt{\frac{\hat{p}(1-\hat{p})}{n}}}\) | \(z\) |
| \(p_1 - p_2\) | two-sample | Categorical | \((\hat{p}_1 - \hat{p}_2)\pm Z_{1-\alpha/2} \sqrt{\frac{\hat{p}_1(1-\hat{p}_1)}{n_1}+\frac{\hat{p}_2(1-\hat{p}_2)}{n_2}}\) | \(\frac{\hat{p}_1 - \hat{p}_2}{ \sqrt{\hat{p}(1-\hat{p})\left(\frac{1}{n_1}+\frac{1}{n_2}\right)}}\) | \(z\) |
| \(\mu\) | one-sample | Quantatitive | \(\bar{x} \pm t_{1-\alpha/2, n-1}\frac{s}{\sqrt{n}}\) | \(\frac{\bar{x} - \mu_0}{s/\sqrt{n}}\) | \(t(n-1)\) |
| \(\mu_1 - \mu_2\) | two-sample | Quantitative | \((\bar{x}_1 - \bar{x}_2) \pm t_{1-\alpha/2, \min(n_1 -1, n_2-1)} \sqrt{\frac{s_1^2}{n_1}+\frac{s_2^2}{n_2}}\) | \(\frac{\bar{x}_1 - \bar{x}_2}{\sqrt{\frac{s_1^2}{n_1}+\frac{s_2^2}{n_2}}}\) | \(t(\min(n_1 - 1, n_2 - 1))\) |
| \(\mu_1 - \mu_2\) | pooled two-sample | Quantitative | \((\bar{x}_1 - \bar{x}_2) \pm t_{1-\alpha/2, \min(n_1 -1, n_2-1)} s_{pooled}\sqrt{\frac{1}{n_1}+\frac{1}{n_2}}\) | \(\frac{\bar{x}_1 - \bar{x}_2}{s_{pooled}\sqrt{\frac{1}{n_1}+\frac{1}{n_2}}}\) | \(t(n_1+n_2 - 2)\) |
| \(\mu_d\) | matched pairs | Quantitative | \(\bar{x}_d \pm t_{1-\alpha/2, n-1}\frac{s_d}{\sqrt{n}}\) | \(\frac{\bar{x}_d - \mu_d}{s_d/\sqrt{n}}\) | \(t(n-1)\) |
Despite significantly expanding the our statistical tools for inference, we are still quite limited in our ability to analyze qualitative responses. Our tests for a proportion are useful for comparing a single category of a qualitative variable across one or two samples, but what if we are interested in comparing multiple categories across more than one population? We will now explore some of the common tools for analyzing qualitative data. The inference techniques for analyzing qualitative variables are generally concerned with comparing a response variable with two or more categories across an explanatory variable with two or more groupings by exploring how the conditional distribution of the response varies across the groups of the explanatory variable. In other words, these inference procedures are designed to analyze the statistical association between two multi-category qualitative variables.
Such problems are typically represented as a table where the rows represent the groupings of the explanatory variable and columns represent the categories of the response variable - often referred to as “two-way tables”.
The Chi-square goodness of fit test
Like we have done with means and proportions, we will begin with a one-sample procedure for comparing the distribution of a categorical variable to some hypothesized model. This procedure is called the \(\chi^2\) (“chi-squared”) goodness of fit test because it used to determine how well the observed distribution fits some proposed model of the data. We will illustrate this idea by starting with an example:
Example: Gregor Mendels Peas - Gregor Mendel conducted a study in which he crossed pea plants. The plants he crossed had the alleles (i.e., a form or version of a gene) for both yellow \(Y\) and green peas \(y\) — a trait controlled by a single locus. He believed two of his laws applied here: the Law of Segregation and the Law of Dominance. These laws would determine the probabilities of certain genotypes. This can be summarized by a Punnett square
| Yellow | Green |
|---|---|
| \(YY = 0.25\) | \(Yy = 0.25\) |
| \(Yy = 0.25\) | \(yy = 0.25\) |
- If Mendel’s Laws are true, what do they imply about the probability distribution for these four outcomes (i.e., \(YY\), \(Yy\), \(yY\), or \(yy\))? And what does this imply about the probability distribution of color (i.e., yellow or green) ?
Mendel bred \(8023\) offspring. Of these, \(6022\) were yellow, and \(2001\) were green. Do his laws “fit” the data? That is, does the trait of color in pea plants exhibit what we would call Mendelian inheritance?
| Color | Expected Frequency | Observed Count | Observed Frequency |
|---|---|---|---|
| Yellow | 0.75 | 6022 | 0.7506 |
| Green | 0.25 | 2001 | 0.2494 |
The above problem amounts to comparing the observed frequencies of each color to the frequencies that we would expect under the Mendelian model of inheritance. We can test whether the data fit Mendel’s model by comparing the observed frequencies of pea plant colors to the frequencies we would expect assuming Mendelian Inheritance and Dominance.
In this case the null hypothesis is that the offspring of the pea plants follows Mendelian inheritance or
\[H_0: p_{yellow} = 0.75; p_{green} = 0.25 \]
The alternative is that one or more of the frequencies for each color do not follow the frequencies defined in the null hypothesis. To generalize for a categorical variable with \(k\) possible outcomes the null becomes \(H_0: p_i = c_i; \forall i\in[1:k]\) and \(H_A:\) at least one \(p_i \neq c_i\).
The above hypothesis test uses a \(\chi^2\) test statistic defined as
\[X^2 = \sum_{i =1}^k \frac{(\text{observed count}_i - \text{expected count}_i)^2}{\text{expected count}_i} \]
\(k\) is the number of possible outcomes
the observed count is the number of observations we observed with outcome \(i\)
the expected count is the number of observations we expect to have outcome \(i\) which is calculated under the null hypothesis as \(np_i\)
We can think of this calculation as measuring the average distance from the observed model to the model we defined under the null hypothesis.
\(X^2\) can take on values between \(0\) and positive \(\infty\). A value of zero means the observed model exactly follows the expected model. Values greater than zero indicate a deviation from the expected model. Large values of \(X^2\) indicate evidence against the null hypothesis.
Referring back to Mendel’s pea plants we compute the expected number of yellow pea plants as \(8023\times 0.75 = 6017.25\) and the expected number of green pea plants to be \(8023\times 0.25 = 2005.75\). The test statistic is
\[X^2 = \frac{(6022 - 6017.25)^2}{6017.25} +\frac{(2001 - 2005.75)}{2005.75} \]
\[ = 0.0037 + 0.0112 \]
\[ \approx 0.015\]
The Chi-square distribution
To convert the above statistic into a \(p\)-value we need to know its sampling distribution. The statistic \(X^2\) is called a \(\chi^2\) (“chi-squared”) test statistic because its sampling distribution follows a special type of probability distribution called the \(\chi^2\) distribution. Like the \(t\) distribution, the \(\chi^2\) distributions form a family of distributions controlled by a single parameter - the degrees of freedom. We will use the notation \(\chi^2(df)\) to depict a specific member of this family. For the goodness of fit test, the test statistic \(X^2\) follows a \(\chi^2\) distribution with \(k-1\) degrees of freedom where \(k\) represents the number of categories of the qualitative variable
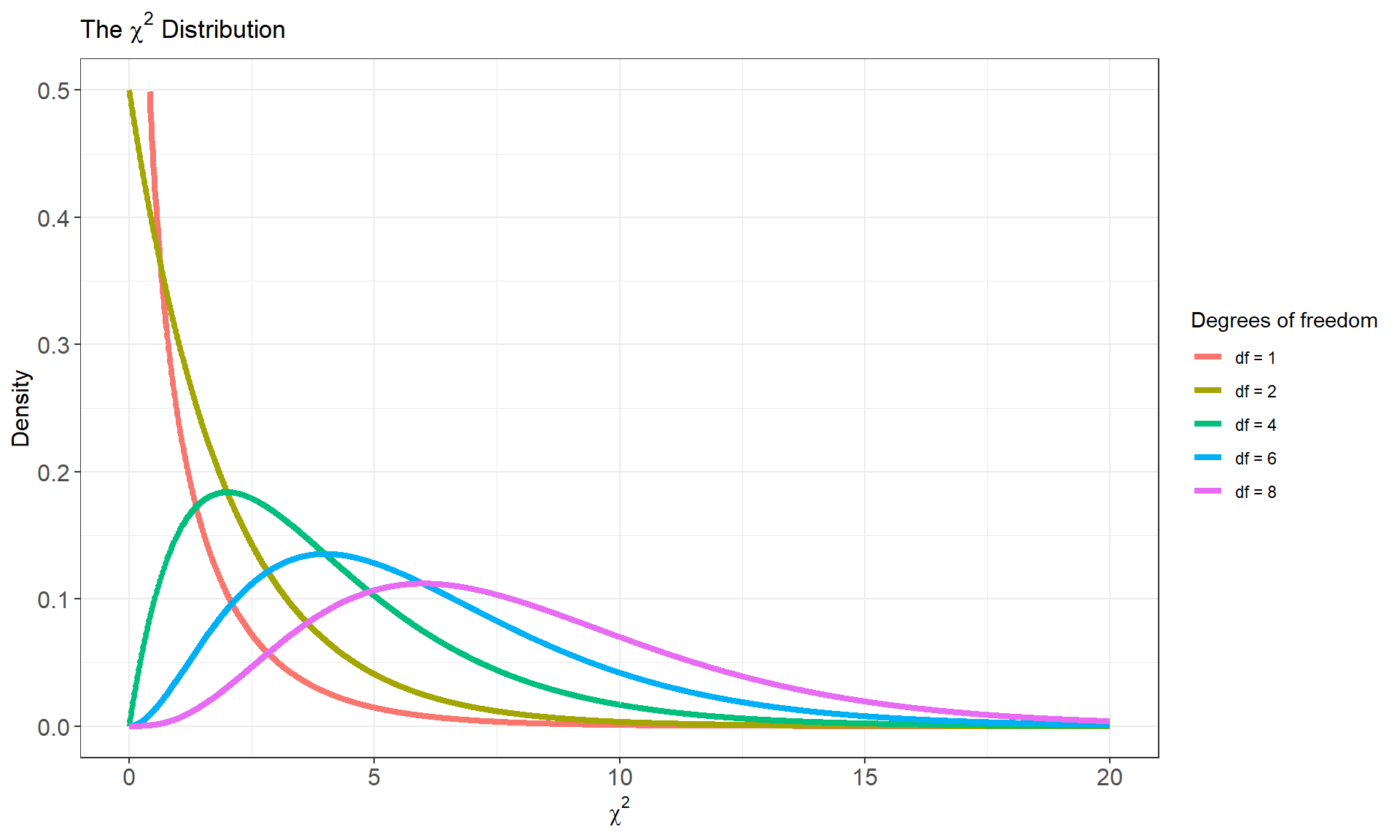 * Note from the graph above that as the degrees of freedom increase the
\(\chi^2\) distribution converges in
shape to a normal distribution.
* Note from the graph above that as the degrees of freedom increase the
\(\chi^2\) distribution converges in
shape to a normal distribution.
Under the special case of a \(\chi^2(1)\) the \(\chi^2\) statistic is equal to the square of a standard normal distribution \(Z^2\).
In general, a \(\chi^2\) random variable with \(k\) degrees of freedom can be represented as a sum of \(k\) squared normal random variables
\[\chi^2_k = \sum_{i = 1}^k Z_i^2 = Z_1^2 + Z_2^2 + \cdots Z_k^2 \]
- Like the \(t\) distribution, we can look up the probability of different chi-squared random variables using the degrees of freedom and a table of pre-computed probabilities:
| Upper tail | 0.25 | 0.2 | 0.15 | 0.125 | 0.1 | 0.075 | 0.05 | 0.025 | 0.005 | 0.0025 | 5e-04 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| \(DF\) | |||||||||||
| 1 | 1.323 | 1.642 | 2.072 | 2.354 | 2.706 | 3.17 | 3.841 | 5.024 | 7.879 | 9.141 | 12.116 |
| 2 | 2.773 | 3.219 | 3.794 | 4.159 | 4.605 | 5.181 | 5.991 | 7.378 | 10.597 | 11.983 | 15.202 |
| 3 | 4.108 | 4.642 | 5.317 | 5.739 | 6.251 | 6.905 | 7.815 | 9.348 | 12.838 | 14.32 | 17.73 |
| 4 | 5.385 | 5.989 | 6.745 | 7.214 | 7.779 | 8.496 | 9.488 | 11.143 | 14.86 | 16.424 | 19.997 |
| 5 | 6.626 | 7.289 | 8.115 | 8.625 | 9.236 | 10.008 | 11.07 | 12.833 | 16.75 | 18.386 | 22.105 |
| 6 | 7.841 | 8.558 | 9.446 | 9.992 | 10.645 | 11.466 | 12.592 | 14.449 | 18.548 | 20.249 | 24.103 |
| 7 | 9.037 | 9.803 | 10.748 | 11.326 | 12.017 | 12.883 | 14.067 | 16.013 | 20.278 | 22.04 | 26.018 |
| 8 | 10.219 | 11.03 | 12.027 | 12.636 | 13.362 | 14.27 | 15.507 | 17.535 | 21.955 | 23.774 | 27.868 |
| 9 | 11.389 | 12.242 | 13.288 | 13.926 | 14.684 | 15.631 | 16.919 | 19.023 | 23.589 | 25.462 | 29.666 |
| 10 | 12.549 | 13.442 | 14.534 | 15.198 | 15.987 | 16.971 | 18.307 | 20.483 | 25.188 | 27.112 | 31.42 |
| 11 | 13.701 | 14.631 | 15.767 | 16.457 | 17.275 | 18.294 | 19.675 | 21.92 | 26.757 | 28.729 | 33.137 |
| 12 | 14.845 | 15.812 | 16.989 | 17.703 | 18.549 | 19.602 | 21.026 | 23.337 | 28.3 | 30.318 | 34.821 |
| 13 | 15.984 | 16.985 | 18.202 | 18.939 | 19.812 | 20.897 | 22.362 | 24.736 | 29.819 | 31.883 | 36.478 |
| 14 | 17.117 | 18.151 | 19.406 | 20.166 | 21.064 | 22.18 | 23.685 | 26.119 | 31.319 | 33.426 | 38.109 |
| 15 | 18.245 | 19.311 | 20.603 | 21.384 | 22.307 | 23.452 | 24.996 | 27.488 | 32.801 | 34.95 | 39.719 |
| 16 | 19.369 | 20.465 | 21.793 | 22.595 | 23.542 | 24.716 | 26.296 | 28.845 | 34.267 | 36.456 | 41.308 |
| 17 | 20.489 | 21.615 | 22.977 | 23.799 | 24.769 | 25.97 | 27.587 | 30.191 | 35.718 | 37.946 | 42.879 |
| 18 | 21.605 | 22.76 | 24.155 | 24.997 | 25.989 | 27.218 | 28.869 | 31.526 | 37.156 | 39.422 | 44.434 |
| 19 | 22.718 | 23.9 | 25.329 | 26.189 | 27.204 | 28.458 | 30.144 | 32.852 | 38.582 | 40.885 | 45.973 |
| 20 | 23.828 | 25.038 | 26.498 | 27.376 | 28.412 | 29.692 | 31.41 | 34.17 | 39.997 | 42.336 | 47.498 |
| 21 | 24.935 | 26.171 | 27.662 | 28.559 | 29.615 | 30.92 | 32.671 | 35.479 | 41.401 | 43.775 | 49.011 |
| 22 | 26.039 | 27.301 | 28.822 | 29.737 | 30.813 | 32.142 | 33.924 | 36.781 | 42.796 | 45.204 | 50.511 |
| 23 | 27.141 | 28.429 | 29.979 | 30.911 | 32.007 | 33.36 | 35.172 | 38.076 | 44.181 | 46.623 | 52 |
| 24 | 28.241 | 29.553 | 31.132 | 32.081 | 33.196 | 34.572 | 36.415 | 39.364 | 45.559 | 48.034 | 53.479 |
| 25 | 29.339 | 30.675 | 32.282 | 33.247 | 34.382 | 35.78 | 37.652 | 40.646 | 46.928 | 49.435 | 54.947 |
| 26 | 30.435 | 31.795 | 33.429 | 34.41 | 35.563 | 36.984 | 38.885 | 41.923 | 48.29 | 50.829 | 56.407 |
| 27 | 31.528 | 32.912 | 34.574 | 35.57 | 36.741 | 38.184 | 40.113 | 43.195 | 49.645 | 52.215 | 57.858 |
| 28 | 32.62 | 34.027 | 35.715 | 36.727 | 37.916 | 39.38 | 41.337 | 44.461 | 50.993 | 53.594 | 59.3 |
| 29 | 33.711 | 35.139 | 36.854 | 37.881 | 39.087 | 40.573 | 42.557 | 45.722 | 52.336 | 54.967 | 60.735 |
| 30 | 34.8 | 36.25 | 37.99 | 39.033 | 40.256 | 41.762 | 43.773 | 46.979 | 53.672 | 56.332 | 62.162 |
| 40 | 45.616 | 47.269 | 49.244 | 50.424 | 51.805 | 53.501 | 55.758 | 59.342 | 66.766 | 69.699 | 76.095 |
| 50 | 56.334 | 58.164 | 60.346 | 61.647 | 63.167 | 65.03 | 67.505 | 71.42 | 79.49 | 82.664 | 89.561 |
| 100 | 109.141 | 111.667 | 114.659 | 116.433 | 118.498 | 121.017 | 124.342 | 129.561 | 140.169 | 144.293 | 153.167 |
| Z-score | 0.674 | 0.842 | 1.036 | 1.15 | 1.282 | 1.44 | 1.645 | 1.96 | 2.576 | 2.807 | 3.291 |
| Confidence Level: | \(50\%\) | \(60\%\) | \(70\%\) | \(75\%\) | \(80\%\) | \(85\%\) | \(90\%\) | \(95\%\) | \(99\%\) | \(99.5\%\) | \(99.9\%\) |
Lecture 28 Friday, April 12th 2024
Warm Up: \(\chi^2\) Goodness of Fit Test - Suppose you’re hired by a dog food company to help them test three new dog food flavors. You recruit a random sample of \(75\) dogs and offer each dog a choice between the three flavors by placing bowls in front of them. Assuming that the dogs have no preference, you expect that the flavors will be equally popular among the dogs, with about \(25\) dogs choosing each flavor. After weeks of hard work, your dog food experiment is complete and you compile your data in a table:
| Flavor | Observed Count | Expected Count |
|---|---|---|
| Garlic Blast | 22 | |
| Bacon Delight | 30 | |
| Chicken Crunch | 23 |
Conduct a \(\chi^2\) goodness of fit test to determine if the dogs show any preference for the three flavors being tested
Note that the GOF test doesn’t tell us anything about the range of plausible valuables for the frequency parameters.
Measureing statistical association in two categorical variables
As stated previously, the goodness of fit test is a one-sample procedure for comparing the observed distribution of a single categorical variable to a specific model that we hypothesize under the null. We will now explore another type of inference which is also based on the \(\chi^2\) (“chi-square”) distribution. This procedure is used to determine if two categorical variables share an association by exploring how the distribution of counts of one variable changes as we condition on the categories of another variable.
\(\chi^2\) test of independence
The \(\chi^2\) test of independence is used to examine the relationship between two categorical variables in a two-way table (also called a contigency table). Consider the following hypothetical table which compares the categorical variable \(A\), which has two categories, with the categorical variable \(B\) which has three categories.
| Variable A | ||||
| Category 1 | Category 2 | Marginal Distribution B | ||
| Category 1 | \(P(\text{Category} \ 1A | \text{Category} \ 1B)\) | \(P(\text{Category} \ 2A | \text{Category} \ 1B)\) | \(\sum_j P(\text{Category} \ jA | \text{Category} \ 1B)\) | |
| Variable B | Category 2 | \(P(\text{Category} \ 1A | \text{Category} \ 2B)\) | \(P(\text{Category} \ 2A | \text{Category} \ 2B)\) | \(\sum_j P(\text{Category} \ jA | \text{Category} \ 2B)\) |
| Category 3 | \(P(\text{Category} \ 1A | \text{Category} \ 3B)\) | \(P(\text{Category} \ 2A | \text{Category} \ 3B)\) | \(\sum_j P(\text{Category} \ jA | \text{Category} \ 3B)\) | |
| Marginal Distribution A | \(\sum_i P(\text{Category} \ 1A | \text{Category} \ iB)\) | \(\sum_i P(\text{Category} \ 2A | \text{Category} \ iB)\) | 1 |
The two-way table above helps us to break down the relationship between the outcomes of Variable A and the outcomes of Variable B. As we can see from the table, the cells give the conditional probabilities (or more often frequencies/counts) of each category of \(A\) across each category of \(B\). There are also usually row and column totals displayed in a two-way table which summarize the marginal distributions of each variable.
A \(\chi\)-square test of independence takes advantage of the two-way table above to determine if the conditional distribution of the response variable (the rows) changes across the categories of the explanatory variable (the columns). In the example above, we can see that each row gives the marginal distribution of a given category of the response variable. If variable A and variable B are independent then the rows of the table should be more or less the same across all categories of the explanatory variable. If the outcomes of variable B depend on the outcomes of variable \(A\), then the rows of the table will change as we move across the outcomes of variable B.
The null and alternative hypothesis of a \(\chi\)-square test of independence are simple. The null hypothesis is that the two variables being tested are independent and the alternative is that they not independent
\[ H_0: \text{Variable A and Variable B are independent} \] \[ H_A: \text{Variable A and Variable B are NOT independent}\]
Like the goodness of fit test, the alternative hypothesis does not specify any particular direction. Because the two-way table can contain all sorts of possible associations, the alternative hypothesis cannot be described as one or two sided.
To test the null hypothesis of “no dependence” between two variables in a table with \(r\) rows and \(c\) columns, we take a similar approach to the goodness of fit test and compare the observed cell counts in all cells of the table to their expected cell counts under the null hypothesis.
In essence we are comparing two tables which represent two distributions: the table of observed cell counts which represents the observed joint distribution of the response and explanatory variables and the table of expected cell counts which represents expected joint distribution of the two variables the null hypothesis of no association.
The test statistic summarizes the differences (i.e distance) between the counts in the observed table with the counts in the expected table.
\[ X_{obs}^2 = \sum_{j=1}^r\sum_{j=1}^c \frac{(o_{ij} - e_{ij})^2}{e_{ij}} \]
Where \(o_{ij}\) represents the observed count for the \(i^{th}\) row and \(j^{th}\) column of the contingency table:
| X. | Category.1 | Category.2 | X..1 | Category.c | Total |
|---|---|---|---|---|---|
| Category 1 | \(o_{11}\) | \(o_{12}\) | \(\cdots\) | \(o_{1c}\) | \(\sum_{j=1}^c o_{1j}\) |
| Category 2 | \(o_{21}\) | \(o_{22}\) | \(\cdots\) | \(o_{2c}\) | \(\sum_{j=1}^c o_{2j}\) |
| ⋮ | \(\vdots\) | \(\vdots\) | \(\vdots\) | \(\vdots\) | \(\vdots\) |
| Category r | \(o_{r1}\) | \(o_{r2}\) | \(\cdots\) | \(o_{rc}\) | \(\sum_{j=1}^c o_{rj}\) |
| Total | \(\sum_{i=1}^r o_{i1}\) | \(\sum_{i=1}^r o_{i2}\) | \(\cdots\) | \(\sum_{i=1}^r o_{ic}\) | \(n = \sum_{i=1}^r\sum_{j=1}^c o_{ij}\) |
The expected counts for \(i,j^{th}\) cell of the table are computed from the observed counts such that
\[ e_{ij} = \frac{ \big[ \sum_{i = 1}^r o_{ij} \big] \times \big[ \sum_{j = 1}^c o_{ij} \big] }{ \sum_{i=1}^r \sum_{j=1}^c o_{ij} } = \frac{\text{row total}\times\text{column total}}{n} \]
The test statistic follows a \(\chi^2\) distribution with \((r-1)\times (c-1)\) degrees of freedom, where \(r\) is the total number of row categories and \(c\) is the total column categories. Lets try it out an example:
Example: Happiness and Income - As part of their annual survey, the General Social Survey explored the relationship between income and happiness. Happiness was recorded as “Not too happy”, “Pretty happy”, or “Very happy”, and incomes were bracketed into three categories: “Below average”, “Average”, and “Above average”. The counts are summarized in the table below:
| Income | Not Too Happy | Pretty Happy | Very Happy | Total |
|---|---|---|---|---|
| Above Average | 29 | 178 | 135 | 342 |
| Average | 83 | 494 | 277 | 854 |
| Below Average | 104 | 314 | 119 | 537 |
| Total | 216 | 986 | 531 | 1733 |
Conduct a \(\chi^2\) test of independence to determine if there is evidence to support that income is related to happiness
- The table of expected counts is given below
| Not Too Happy | Pretty Happy | Very Happy | |
|---|---|---|---|
| Above Average | \(\frac{342\times 216}{1733} = 42.63\) | \(\frac{342\times 986}{1733} = 194.58\) | \(\frac{342\times 531}{1733} = 104.79\) |
| Average | \(\frac{854\times 216}{1733} = 106.44\) | \(\frac{854\times 986}{1733} = 485.89\) | \(\frac{854\times 531}{1733} = 261.67\) |
| Below Average | \(\frac{537\times 216}{1733} = 66.93\) | \(\frac{537\times 986}{1733} = 305.53\) | \(\frac{537\times 531}{1733} = 164.54\) |
- the table below gives the squared deviations across all cell counts
| Not Too Happy | Pretty Happy | Very Happy | |
|---|---|---|---|
| Above Average | \(\frac{(42.63 - 29)^2}{42.63} = 4.36\) | \(\frac{(194.58 - 178)^2}{194.58} = 1.41\) | \(\frac{(104.79 - 135)^2}{104.79} = 8.71\) |
| Average | \(\frac{(106.44 - 83)^2}{106.44} = 5.16\) | \(\frac{(485.89 - 494)^2}{485.89} = 0.14\) | \(\frac{(261.67 - 277)^2}{261.67} = 0.9\) |
| Below Average | \(\frac{(66.93 - 104)^2}{66.93} = 20.53\) | \(\frac{(305.53 - 314)^2}{305.53} = 0.23\) | \(\frac{(164.54 - 119)^2}{164.54} = 12.6\) |
The \(\chi^2\) test statistic can be computed as the sum of the elements in the table above
\[ X_{obs}^2 = 4.36 + 5.16 + \cdots +0.23 + 12.6 = 54.04 \]
which follows a \(\chi^2\) distribution with \((3-1)\times (3 - 1) = 4\) degrees of freedom. The \(p\)-value is the probability of observing a value more extreme than \(X_{obs}^2 = 54.05\) which is
\[P(\chi^2_4 \geq 54.04|H_0 \ \text{True}) \approx 0 \]
Thus, at \(\alpha = 0.05\) level we would conclude that there is significant evidence that income and happiness are related.